What do 13, 37, 41 and 91 have in common? They are all cycling numbers*!

What are cycling numbers? Try this trick about the number 37: • Take a three-digit multiple of 37 (for example 481). It will be more interesting if all the digits of your multiple are different. • ‘Cycle’ it (re-write it so one of the other digits is first but so the digits are still in the same order). For the example above you could create 814 or 148. • Now divide your new number by 37, and you will find you get an integer.
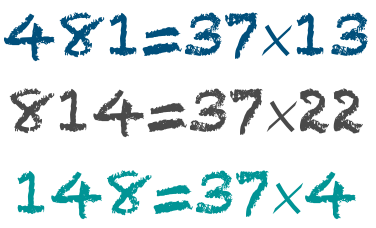
The number you created by ‘cycling’ your multiple of 37, is also a multiple of 37!
Wow! Why does this work? Can you prove why this works for all three-digit multiples of 37? (Spoilers below!)
A while ago a friend told me about this curious property of three-digit multiples of 37 and I started to play around with it, trying to work out why this happens. I found an algebraic proof, which led me to find other numbers whose multiples have this property too.
I am defining cycling numbers to be any numbers in this family; numbers for whom all of their multiples of a specific length (in the case of 37 the multiples have to be three-digits) can be ‘cycled’ any number of places and give a result that is still a multiple of that cycling number.
There are an infinite number of cycling numbers! Every prime number apart from 2 and 5 is a cycling number. But I have a personal favourite: 41. Make any five-digit multiple of 41 and ‘cycle’ it any number of places. You will find that the number you have created is also a multiple of 41.
My proof that all three-digit multiples of 37 can be ‘cycled’ is below.
We can express a three-digit number as:
100a + 10b + c (where a, b and c are any positive integers)
As our number is a multiple of 37 the following is true:
100a + 10b + c = 37m (m is some positive integer)
When we cycle the number just one place, we get the number:
100b + 10c + a
Below, I have expressed the new number as the original number plus some difference:
100b + 10c + a = 100a + 10b + c + [−99a +90b + 9c]
new number = original number + [−99a +90b + 9c]
new number = 37m + [−99a +90b + 9c]
If (and only if) the difference ‘-99a + 90b + 9c’ is a multiple of 37, then the new number will also be a multiple of 37.
We can show this is the case by writing the difference in terms of the original number:
−99a +90b + 9c = (900a + 90b + 9c) − 999a
= 9(100a + 10b + c) − 999a
= 9(37m) − 37(27a)
= 37(9m − 27a)
The difference is a multiple of 37, and therefore the new number is a multiple of 37.
My proof imagines the number is being ‘cycled’ only one place. But ‘cycling’ one place repeatedly will also result in a multiple of 37. And ‘cycling’ one place repeatedly is the same as ‘cycling’ multiple places in one go, so our proof applies to ‘cycling’ any number of places.
37 is not the only cycling number for three-digit multiples! In the proof we were able to show 37 is a factor of the difference because it is a factor of 999 (and because we made our original number a multiple of 37). We could show that any other factor of 999 is a cycling number if we start instead with an original number that is a multiple of that number. All factors of 999 (apart from 1!) are cycling numbers.
Writing 999 as a product of its primes gives: 999 = 3 × 3 × 3 × 37
We can see that the prime cycling numbers (for three-digit multiples) are 3 and 37. This prime decomposition dictates which composite numbers will be cycling numbers.
The discovery that 3 and 9 are cycling numbers is not astonishing; we would expect 3 and 9 to be cycling numbers given their digit sum property. Multiples of 3 or 9 have digit sums that are themselves multiples of 3 or 9, respectively. This property means we can do more impressive things than the cycling trick; we could write the digits of a multiple of 3 or 9 in any permutation at all (without the restriction that they stay in the same order) and we would end up with a multiple of 3 or 9 still, because the digit sum would remain unchanged.
Thus I declare 37 the most interesting cycling number for three-digit multiples! But it doesn’t stop there! What about four-digit multiples? Or n-digit multiples? The same proof can be applied to numbers with higher numbers of digits. The difference between the new number and the original number will have the same structure as above, but with additional terms.
For example, for a four digit number the difference can be expressed as:
−999a +900b + 90c + 9d
= (9000a + 900b + 90c + 9d) − 9999a
= 9(1000a + 100b + 10c + d) – 9999a
where 1000a + 100b + 10c + d is the original number.
And this time any factors of 9,999 are cycling numbers. As we would expect, we can see that 3 and 9 are cycling numbers for any number of digits, as a string of 9s of any length with always have 9 as a factor.
We can find which of the primes (other than 3) cycle for four digit numbers by just looking for the prime factors of 1,111.
We can re-write the difference as: = 9[(1000a + 100b + 10c + d) – 1111a]
And for five-digits we’d be looking for prime factors of 11,111, and so on.
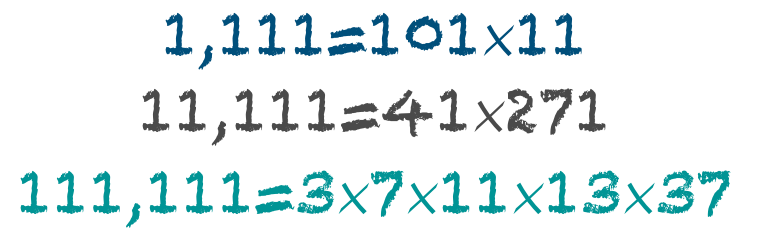
I challenge you to investigate cycling numbers further and make your own cycling number trick.
*According to me: if anyone else has a different name for the numbers this article is about, I’d like to know! (Not to be confused with cyclic numbers – which are connected, and arguably more interesting.)